[LeetCode] 42. Trapping Rain Water

1ilsang
클라이밍 하실래염?
#algorithm#leetcode#hard#stack#two-pointers
Published

cover

문제 링크

빗물이 고일 수 있는 모든 영역을 구하면 되는 문제다.

기본적으로 물은 '높은 곳에서 낮은 곳'으로 흐르기 때문에 우리는 높이를 비교하면서 빗물이 고일 수 있는지 판단해야 한다.

이 문제는 두 가지 스택과 투포인터 두 가지로 풀 수 있다. 두 방법 모두 알아두면 좋기 때문에 두 가지 해석을 모두 하려고 한다.

접근법 1. Stack O(n) T(n)

스택 접근은 "가로로 면적을 합해가는" 방식이다.

빗물이 고이기 위해서는 양쪽으로 벽이 있어야 한다.

스택을 활용해 양 벽을 계산하는 방법은, 높이가 감소할 때는 스택에 푸쉬하고 높이가 이전 탑보다 높아질 때는 팝을 하면서 얼마만큼의 빗물을 저장할 수 있는지 계산하면 된다.

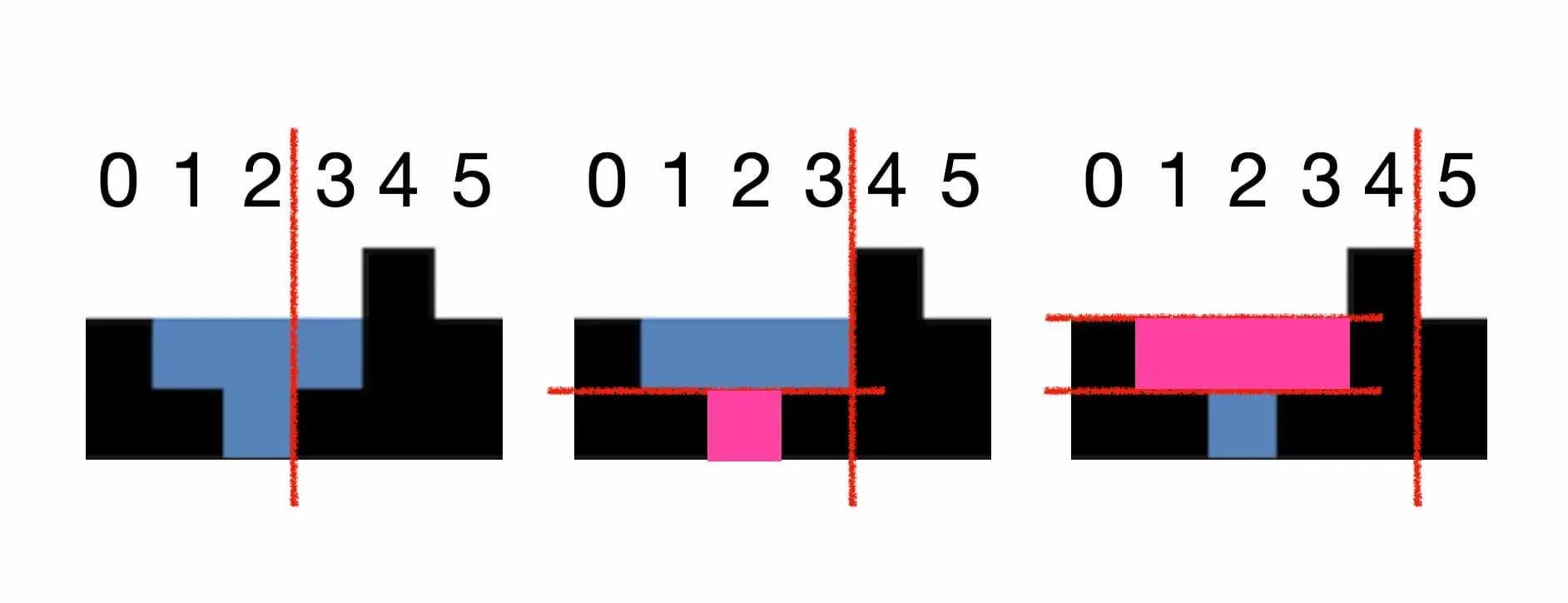
example

0번째 높이부터 순회해 보자.

  1. 모든 원소를 순회할 때마다 스택에 푸쉬한다. 왼쪽의 그림과 같이 높이가 감소해 나갈 때에는 특별한 작업 없이 계속 진행한다.
  2. 중앙의 그림(i = 3)의 상황일 경우 현재 벽이 스택의 Top 값보다 더 높기 때문에 빗물이 고일 수 있다. 현재 높이와 같거나 클 때까지 스택에 쌓여있는 벽들을 pop 하며 "가로로" 누적값을 더한다. 여기서는 높이 1이 최대이므로 스택에 추가된 높이 2(i = 0)까지 계산하지 않고 끝난다.
  3. 우측의 그림(i = 4)에서도 동일하다. 현재 높이보다 큰 높이가 나올 때까지 팝을 하며 계산한다. 2번에서 이미 높이 1일 때의 경우를 계산했으므로 높이 2일 때의 가로 값만 계산하면 된다.

마지막 노드까지 위의 방식을 계속해서 하면 모든 면적을 구할 수 있다. 코드와 라인별 해석은 제일 아래에 작성해 두었다.

접근법 2. Two Pointers O(n) T(1)

투포인터 접근은 "세로로 면적을 합해가는" 방식이다.

빗물이 고이기 위해서는 양쪽으로 벽이 있어야 한다.

투포인터는 양끝에 포인터를 설정하고 좌우로 움직이며 높이가 더 높은 쪽을 향해 간다. 높이가 높은 쪽을 향해 양 포인터를 옮기면 반대로 낮은 쪽은 빗물이 고이는 곳이기 때문에 세로로 더해나가면 된다.

example

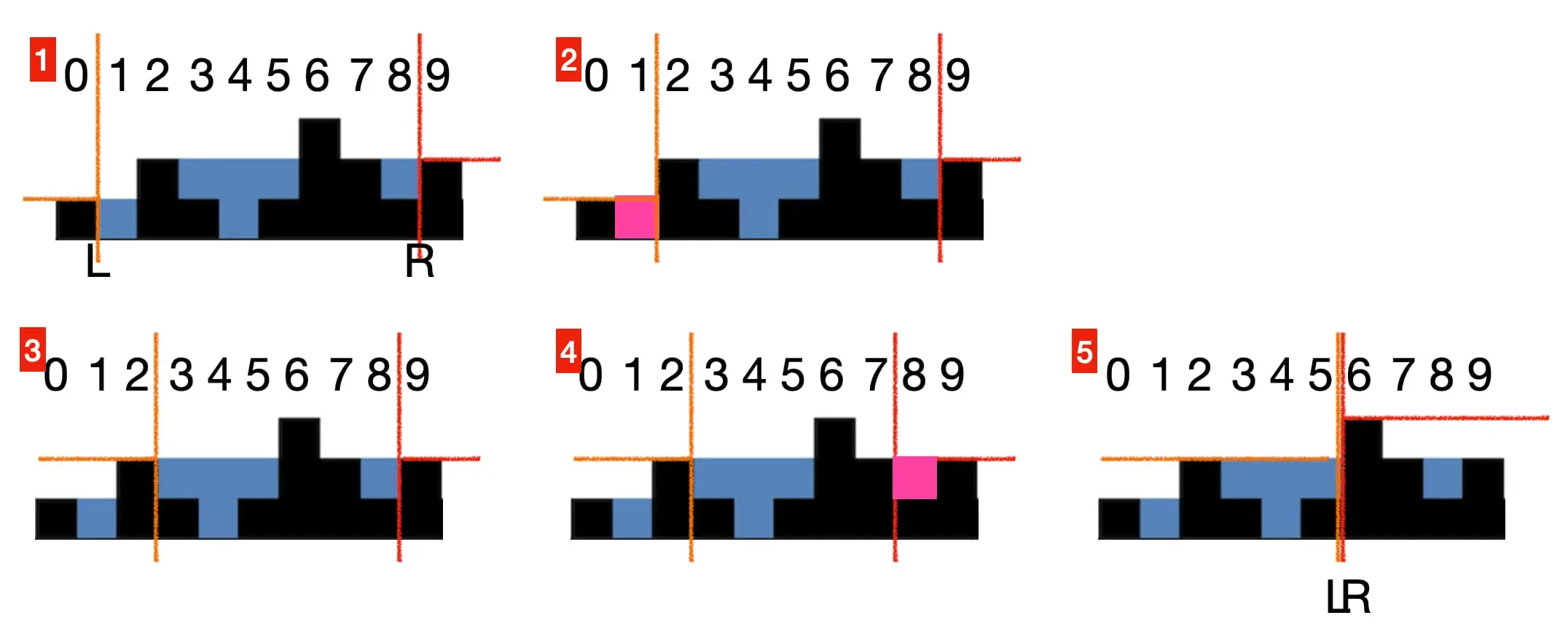
L, R을 양 끝에 두고 순회하면서 각각 MAX 값을 구한다.

  1. 최초의 상태. 최대값(가로선)을 설정한다.
  2. L < R이라면 L을 옮기고 아니면 R을 옮긴다. 여기는 L를 옮겼다. i = 1의 높이가 L의 최대높이보다 낮으므로 그 차이를 더한다.
  3. L < R일 때까지 L을 옮긴 모습이다.
  4. R을 옮겼다. i = 8의 높이가 R의 최대높이보다 낮으므로 그 차이를 더한다.
  5. 계속해서 반복하면 결국 LR은 한곳으로 모이고 그 사이의 모든 세로 값이 더해져 빗물의 면적을 구할 수 있다.

최종 코드

// Stack
const trap = (height) => {
  let res = 0;
  let i = 0;
  const stack = [];
 
  while (i < height.length) {
    const curHeight = height[i];
    // 현재 높이가 스택의 마지막 높이보다 높다면
    while (stack.length > 0 && height[stack[stack.length - 1]] < curHeight) {
      const lastI = stack.pop();
      // 스택이 비었다는 의미는 자신뿐이므로 빗물이 고일 수 없기 때문에 탈출한다.
      if (stack.length === 0) break;
      const peekI = stack[stack.length - 1];
      // 현재 위치(i)와 스택의 다음 위치(peekI)의 거리를 구한다.
      const dist = i - peekI - 1;
      // 현재 위치의 높이와 스택의 다음 위치 높이중 낮은 값을 기준으로 스택의 마지막 높이를 뺀다.
      // 마지막 높이만큼은 빗물이 고일 수 없기 때문
      const h = Math.min(curHeight, height[peekI]) - height[lastI];
      res += dist * h;
    }
    stack.push(i++);
  }
 
  return res;
};
// Two-pointers
const trap = (height) => {
  let res = 0;
  let l = 0;
  let r = height.length - 1;
  let lMax = 0;
  let rMax = 0;
 
  while (l < r) {
    const curLeft = height[l];
    const curRight = height[r];
    // 매번 max 값을 갱신한다. 그래야 자신이 줄어든 값인지 비교할 수 있다.
    lMax = Math.max(curLeft, lMax);
    rMax = Math.max(curRight, rMax);
 
    // 현재 높이가 최대값 보다 적다면 고일 수 있으므로 추가한다.
    if (curLeft < lMax) {
      res += lMax - curLeft;
    }
    if (curRight < rMax) {
      res += rMax - curRight;
    }
    // 양쪽의 포인터를 비교해서 높이가 더 큰 방향으로 이동한다.
    curLeft < curRight ? l++ : r--;
  }
 
  return res;
};
📮 이 포스트에 관심 있으신가요? 이슈를 남겨주세요! 👍
☕ 소주 한 잔 후원하기
(예금주: 이상철)tosskakao