[구름톤 챌린지] 이진수 정렬
1ilsang
클라이밍 하실래염?
Published
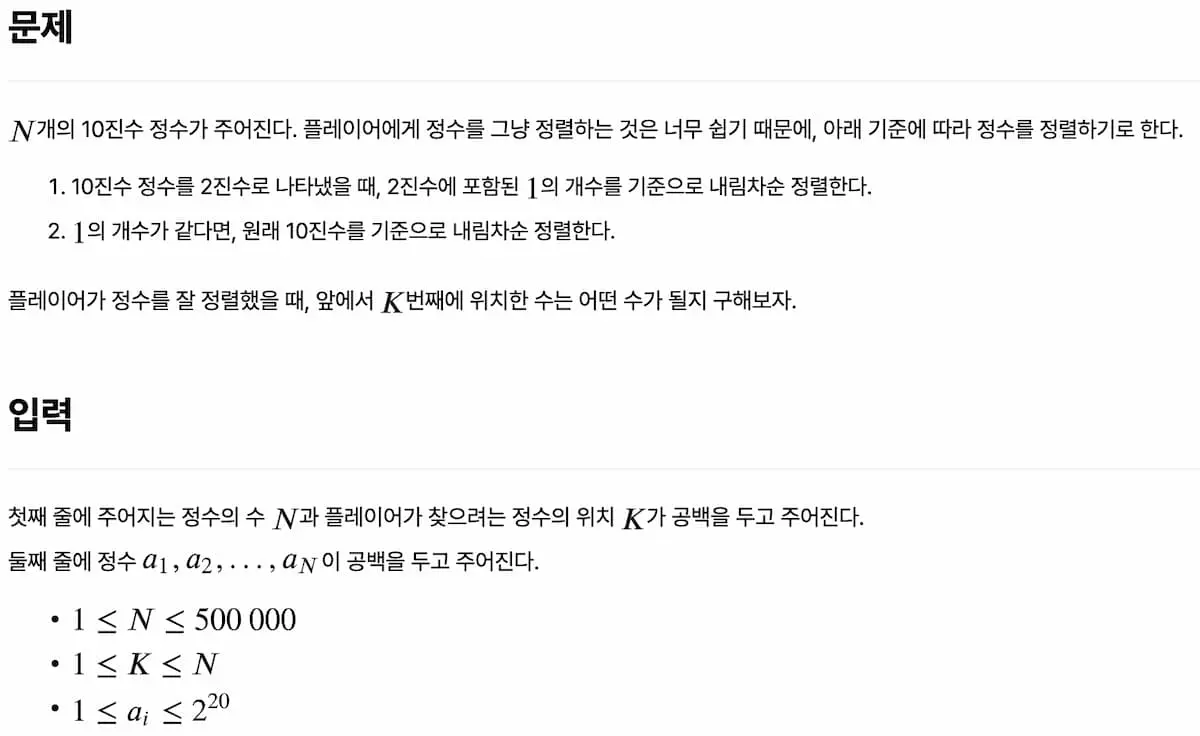
10진수 숫자를 2진법으로 변환후 1의 개수가 가장 많은 순부터 정렬해 K번째 위치 값을 출력하면 되는 문제다.
접근법
N을 순회하면서 각각 2진수로 변환하고 그 값을 저장해 나간다면(O(N^2)) 너무 재미없다.
따라서 우리는 메모를 사용해 이전 값을 활용해 다음 값을 구해 나갈 것이다. 이 방법을 사용하면 O(N)으로 처리가 가능하다.
// 숫자별 1의 개수를 정리해 본다.
// Index: [0,1,2,3,4,5,6,7,8,9];
// Count: [0,1,1,2,1,2,2,3,1,2];9까지의 수를 2진수의 개수로 표현하면 위의 표와 같아진다. 여기서 우리는 두 가지 패턴을 찾을 수 있다.
- 2의 지수승(2^n)은 무조건 1이다(1, 2, 4, 8은 2진수에서 무조건 1이다).
- 현재 값에서 2를 나눈 값의 1의 개수와 현재 값을 2로 나눈 나머지를 더하면 현재 값의 1의 개수가 된다.
7을 기준으로 해보자.
7/2 = 3 => 2
7%2 = 1
=> 7 = 3- 7을 2로 나누면 3이 된다. 위의 표에서 3의 1 개수는 2이다.
- 7을 2로 나눈 나머지는 1이다.
- 2 + 1 = 3이므로 7은 3이 된다.
이전 값을 알면 현재 값을 손쉽게 구할 수 있게 되었다.
그러므로 2부터 포문을 돌리면서 메모 배열을 만들고 최댓값을 찾아나가면 된다.
정리
- 메모이제이션을 활용해 들어올 수 있는 숫자의 최댓값
2^20(1048576)까지 이진수의 개수를 구한다. - N을 메모이제이션 배열로 정렬한다.
- K 번 인덱스의 값을 출력한다.
최종 코드
let N, K;
rl.on('line', (line) => {
if (typeof N === 'undefined') {
const [n, k] = line.split(' ').map((num) => Number(num));
N = n;
K = k;
return;
}
const nums = line.split(' ').map((num) => Number(num));
const memo = [0, 1];
// 메모 처리
for (let i = 2; i <= 1048576; i++) {
const before = memo[Math.floor(i / 2)];
const remain = i % 2;
memo[i] = before + remain;
}
// input을 순회하면서 메모 값을 기준으로 정렬한다.
const sortedList = nums.sort((a, b) => {
const am = memo[a];
const bm = memo[b];
// 만약 메모 값이 같다면(1의 개수가 동일하다면) 10진수를 기준으로 정렬
if (am === bm) {
return b - a;
}
return bm - am;
});
console.log(sortedList[K - 1]);
rl.close();
});